好了,前面我们说到了词法分析的过程。如果你按照我的思路进行的话,现在你已经可以把源代码转换成一个一个的词法单元,也就是所谓的token了。接下来要做的就是按照我们人为设定好的语法规则把这些词法单元组织起来。我们前面说过,Mao语言的语法结构极其简单,只有声明变量、表达式和print输出三个部分。而表达式所包含的内容也只包括加减乘除和括号。更关键的是它是保证输入的代码不会出错的。(当然你要满足程序对于健壮性的要求那就是另一回事了)
首先从变量的声明开始讨论起。Mao语言里只有int和double两种类型。所以我们可以一句一句地读取,直至分号结束。
struct token tkindex;
while (!istokenend(tkindex = gettoken())) {
/* 你要记住这是伪代码,不要问我这个函数怎么来的 */
if (tkindex.type == TOKEN_INT) {
while (!istokenend(tkindex = gettoken())) {
if (tkindex.type == TOKEN_VARIABLE) {
/* 把这个名字和类型加到变量列表里 */
} else if (tkindex.type == TOKEN_COMMA) {
/* 如果是逗号,继续前进 */
continue;
} else if (tkindex.type == TOKEN_SEMICOLON) {
/* 遇见分号,声明语句结束,循环停止 */
break;
}
}
} else if (tkindex.type == TOKEN_DOUBLE) {
/* 跟上面一样玩 */
} else if (/* 其他类型 */) {
/* 其他的处理代码 */
}
}为什么可以写得这么简单?因为变量声明的时候保证没有带等号的初始化语句哦。
变量定义还是很简单的事情,重头戏在于表达式的求值。就算是后面的print语句,你不能保证它不会给你来个(注:有同学指出需求文件里只说了print不会输出表达式,只会输出变量,这样就更容易咯)print(a+b)或者直接print(1*3/2),所以要先把表达式求值做好才能实现输出语句。
如何给表达式求值呢?参考文档里给的暗示方法,是把中缀表达式转换为后缀表达式(逆波兰表示法),其中要用到所谓的调度场算法。然后利用栈来求解。这个方法不难,不过我们这里为了程序的可扩展性和方便理解,决定采用树的方式来实现。并且这里的树还是最简单的一种情况,即二叉树。如图:
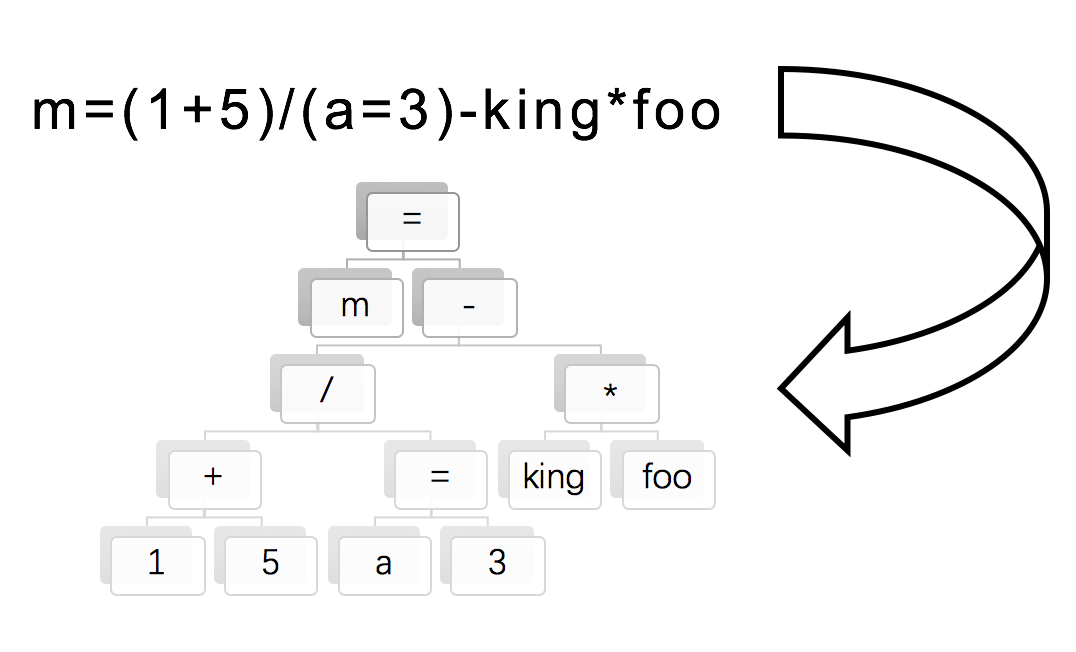
所以,你以为我会这样老老实实写个结构:
struct expr_node {
int type;
char * var_name;
union {
int ival;
double dval;
};
struct expr_node * left_child;
struct expr_node * right_child;
};哼哼,想错了。在这个话题上,为了说明问题,我们用不着那么麻烦。
我在软件工程学生如何学好C语言?这个问题的回答里面说过,理解数据结构不要过分机械地非要做一堆结构体和指针来模拟。计算机科学的核心是抽象。把握好抽象然后再来特化到适合特定场合的结构。所以呢,还是用数组吧。
什么?数组不是顺序存储的结构吗?naive,我们可以这样定义:
- 数组的第一个元素,可以看作整个树的头
- 对于任意第n个元素,它的左子节点是第2n个元素,右子节点是第2n+1个元素
- 类似地,对于任意第n(不论奇偶)个元素,它的父节点编号是n/2
对于这棵树,我们可以稍微分析一下。这棵二叉树每一“层”包含的元素数量是2^n个。所以我们给这个等比数列求一个和,结果就是2^n – 1次方。也就是说对于一个10层的二叉树,我们需要1023个空间的数组。其实也不是很大,而且我们也不太可能出现一个需要10层的表达式数……好吧,如果你实在不放心,C99标准支持以变量初始化数组,自己先感受一下再开数组吧。
好了,数据结构准备好了,我们可以开始构建这个树了。讲道理说语法树有点言过其实,我们这里构建树的过程连什么LL(1)都用不到。我们来思考一下,假如我是一台计算机,我要怎么计算公式k * (a+c) + (j=3)呢?
你也许会说,我们从k开始,k右边的第一个符号就作为树根。但是加减乘除是有优先级的,最后算的应该是加号。注意,我们给这个表达式树求值是自上而下递归求值的,我们把下层计算好之后再把结果返回给上层来计算。所以我们应该以哪个符号开始呢?嗯,第一个优先级最低的符号。在这里,我们的最低优先级的符号是等号,其次是加减,最后是乘除。
等等,貌似有点不对。对于上面的那个等式,如果我们要搜到第一个优先级最低的符号也就是等号,那逻辑不对啊。嗯,因为上面我们没有考虑到括号。所以修正一下上面的规则——第一个括号之外的优先级最低的符号。你需要定义一个变量来记录当前是否外面还有括号。唔,是“第一个”吗?我想应该是最后一个吧,因为在你搜索到最后一个优先级最低的符号之前,是不知道当前位置上的符号是不是最后一个的。像a=1+1这种当然好判断,有等号就行了,可是比如a*21/b+11我怎么知道后面还有没有更低的呢?所以,应该改成——最后一个(括号之外的(优先级最低的(符号)))。(打括号是为了好断句)
好了好了,我们已经把“寻找树根”的任务搞定了。任务已经完成了一半了。什么,你不相信?我们构造这个树是递归的喂!我们只要找到树根,然后正确分划,这个树就搞定了。这就是递归的力量。So,我们再来讨论分划的问题。其实分划挺简单的,我们已经找到了那个“树根”的token,然后parse它左边的部分和右边的部分。
空话说得太多没用,我们来讨论下具体的实现。根据上文的思考,我们可以总结出从token流产生语法树的若干规则:
- 如果整个串中只有一个token,是数或者变量,那么这个表达式树的值就是这个数或者变量的值
- 否则,当前表达式树的值是左子树的值同右子树的值经过计算的结果,计算的方式由树根类型决定
- 树根定义为当前token流中不在任何括号内的最后一个优先级最低的符号,左子树是从token流开始一直到树根的所有内容,右子树同理
- 如果有括号,把括号内内容当作一个整体
由于叙述需要严谨性,所以听起来很复杂。其实整个的实现过程非常的清晰明了,我们来举个例子说明:
对于表达式foo = sample * (3 + 5)而言,我们的搜索过程是这样:
- 从左至右找到最后一个不在括号内的最低优先级符号“=”,将其作为树根。
- 树根左边的子token流里只有一个变量foo,所以左子树的值就是foo,停止。
- 树根右边最后一个不在任何括号内优先级最低的运算符是“*”,将其作为子树的树根。
- 子树树根的左边的token流也只有一个内容,就是sample变量,所以同样停止搜索。
- “*”右边的括号是一个整体,我们在括号内部搜索不在任何“括号”(打引号是因为这里的“不在”是指不在这个括号内部的另外的括号里)内的最低优先级运算符,找到了,是“+”。
- “+”左右都各是一个数,所以这两个子树停止搜索。
如果把这棵二叉树表达为一个数组,我们的数组结构是这样(编号表示下标,C语言的话要全部减1):
- 符号 =
- 变量 foo
- 符号 *
- (空)
- (空)
- 变量 sample
- 符号 +
- (空)
- (空)
- (空)
- (空)
- (空)
- (空)
- 数值 3
- 数值 5
之所以会有那么多空位是因为数或变量是没有子节点的,而数组的话必须要把它们的空间留足。好了,我们解决了理论上生成树的问题,如何用代码来实现呢?首先要面对的一个问题是,不管我们如何递归处理这个表达式,它始终都是一个整体,比如上面,当我们在创建符号“*”的左右子树的时候,为什么不会搜索到“=”那里去呢?所以我们需要两个变量,来标记我们可以搜索的token范围。如果你觉得我说的话很晦涩的话,那是因为我没说清楚。想想子字符串吧,一样的道理。
struct expr_node tmp_tree[128];
struct token stream[1000];
/* stream数组假设已经经过了词法分析阶段的输入 */
/* 为了说明问题,我才使用的全局变量 */
void create_tree(size_t tkstart, size_t tkend, size_t tree_root)
{
if (tkstart == tkend) {
/* 如果整个流只有一个内容 */
if (stream[tkstart].type == TOKEN_INTNUM) {
tmp_tree[tree_root].type = TOKEN_INTNUM;
tmp_tree[tree_root].var_name = NULL;
tmp_tree[tree_root].ival = atoi(stream[tkstart]);
/* 结构体中的匿名联合体是C11标准支持的新语法,可以直接访问它的内部成员 */
/* 这里我们假设在词法分析阶段对于数保存的是它们的字符串形式 */
} else if (stream[tkstart].type == TOKEN_DOUBLENUM) {
/* 同样处理double的情况 */
} else if (stream[tkstart].type == TOKEN_VARIABLE) {
/* 变量的情况也是类似,只不过需要保存它们的名字 */
}
}
int parentheses = 0;
size_t lowest_token = tkstart;
/* 在没有出问题的情况下,第一个token不可能是运算符,所以可以专门规定非运算符的运算符优先级最高 */
for (size_t i = tkstart; i <= tkend; ++i) {
if (is_operator(stream[i])) {
if (priority(stream[i]) < priority(stream[lowest_token] &&
!parentheses) {
/* is_operator和priority都是自己定义的宏 */
lowest_token = i;
}
} else if (stream[i].type == TOKEN_LPAREN) {
/* 左括弧,标记变量加一 */
++parentheses;
} else if (stream[i].type == TOKEN_RPAREN) {
--parentheses;
}
}
create_tree(tkstart, lowest_token - 1, tree_root * 2);
create_tree(lowest_token + 1, tkend, tree_root * 2 + 1);
}这段构造树的代码原理清晰,但是其实它是有问题的:
- 如果一个表达式整个被括号包住,那么它是无法处理的,因为自始至终变量parentheses不为0
- Mao语言的文档里有写
y=(c+6)*-(1+1)这样的表达式,而我们的程序无法处理两个符号连在一起的情况
解决第一个问题,可以用一个简单粗暴但是很脏的办法。所有带括号的表达式,最后都会递归到一个括号从前往后包住的形式。所以如果我们发现第一个token是左括号,我们识别一下是不是从头到尾都被包住了,如果是,就再去掉括号往下识别。
第二个问题,要解决需要我们在识别lowest_token的时候修改一下算法。所谓’+’和’-‘,如果前面有其他非括号的符号,那必然是正负号,否则是加减号。所以,如果发现加减的上一个有运算符,那就把正负号连上作为子树。然后,如果开头是加减号,那就自动补0.
计算的话,很简单的。用一个switch…case语句分开判断当前是什么符号,default表示是数或变量。类型转换的事情交给编译器就好,你要负责的只是判断这个变量应该是什么类型。什么,一个函数不能返回多种类型的值?那可以返回struct嘛,哈哈哈……
发表回复